Part 2
In Part 1, we looked at the theory behind the financial aspects of buying and owning vs. renting. If you haven't read this part yet, bookmark this post here and read part 1 first. You can find part 1 here: https://app.getquin.com/activity/FoLdCxttXY
In Part 2, we'll use these basics and theoretical principles to work through a practical example. It will help you to better apply the calculations to your individual situation. It also provides an impressive illustration of the huge sums involved:
- Detailed calculation of an example (scenario 1)
- Step-by-step adaptation of this example to make it gradually more realistic (scenarios 2 to 6)
tl;dr
I compare the financial burden of a tenant and a buyer in Regensburg over a period of 60 years. Two similar houses - one for rent and one for sale - were selected on immoscout and used as a basis. The variables (increase in rental prices, development of a global portfolio, maintenance reserves, ...) were chosen as they can be assumed to be probable based on the explanations in Part 1 (in Part 3 we look at the effects of the adjustments to these variables: https://app.getquin.com/activity/GEBmMewkKS). This scenario will be adjusted in the course of the article so that it corresponds more closely to reality. This includes, for example, an optimization of the follow-up financing and the assumption that a tenant lives more in line with demand than a buyer, i.e. moves more frequently into a property that suits their life situation.
In the most likely scenarios 5 and 6, the tenant's assets at the end of the period under consideration are several million euros higher than the buyer's assets. Buying such a property in Regensburg and comparable cities is therefore a very expensive decision. From a financial point of view, a purchase is therefore not recommended - as long as the general conditions do not clearly turn in favor of the buyer. In Part 3, we look at what needs to happen for this recommendation to be overturned.
Selection of properties
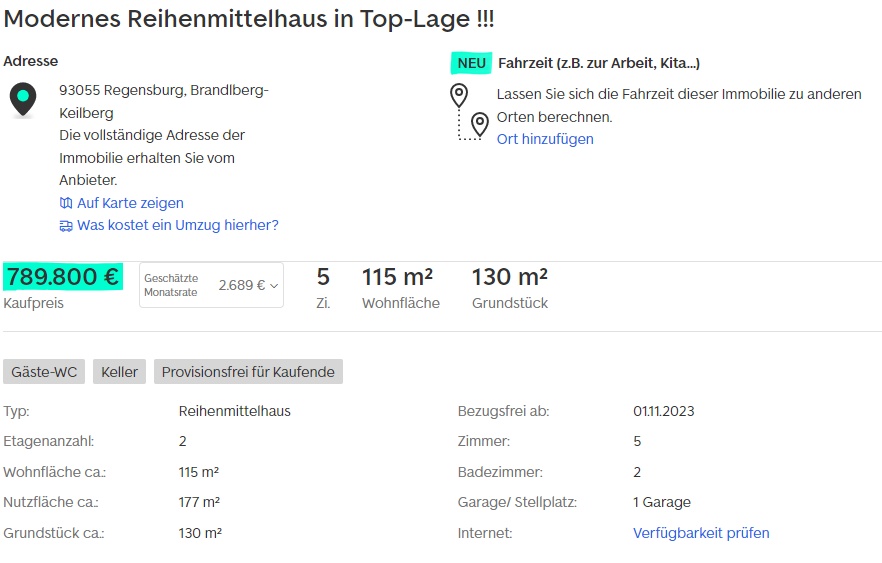
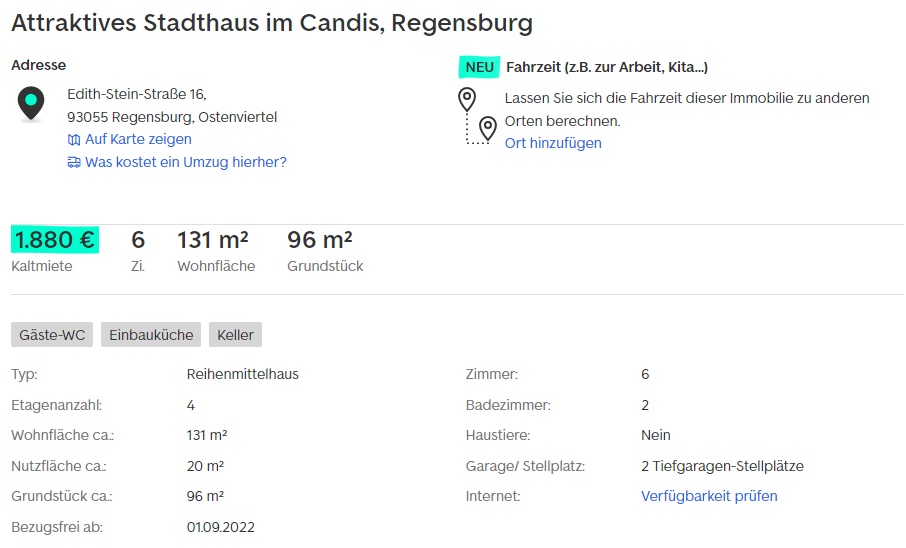
We are looking for a house in Regensburg with enough space for a couple with two children who are due to be born in the next few years. An office is also required. The couple are not gifted craftsmen, which is why the house should be relatively new. As they both earn well, a young building is financially viable. They also wanted to do without gas or oil heating if possible. Two comparable offers were actually found - one for rent and one for sale (see pictures at the end of the article). The house for rent is somewhat more centrally located, offers an additional room, an additional parking space for a car and a larger living space (131m² vs. 115m²). The house for sale is 4 years younger and has a larger plot. Both houses are mid-terrace houses that are heated with district heating and have a fitted kitchen. Overall, the couple like the rented house a little better and would be prepared to spend more money on it. However, the two properties are similar enough for this comparison. In order not to make this detailed example too complex, we assume that the couple will live for another 60 years and remain in the same property until then (this assumption is removed in scenarios 5 and 6). The data was retrieved from Immoscout on 15.06.22 - yes, I've been writing this post for a while.
Scenario 1 - a simple calculation example
The basic rent is 1,880 euros plus 80 euros for two parking spaces, i.e. a total of 1,970 euros. The deposit amounts to 4,400 euros. The house for sale was advertised for 789,800 euros. In addition, there are costs of 30,000 euros for the garage, making a total of 819,900 euros. The couple managed to negotiate the seller down to 750,000 euros. They had saved up 200,000 euros in equity.
Calculation of the purchase and loan costs
The house is located in Bavaria, which is why the following ancillary purchase costs are incurred:
- Real estate transfer tax 3.5%
- Notary fees 1.5%
- Land register entry 0.5%
- Estate agent's fee 3.57
2,000 euros are due for a surveyor. The full purchase costs therefore amount to 750,000 euros * (1 + 0.035 + 0.015 + 0.005 + 0.0357) + 2,000 euros = 820,025 euros. After deducting the equity, a loan of EUR 820,025 - EUR 200,000 = EUR 620,025 must be taken out.
The couple gets a loan with a nominal interest rate of 2.65% and can raise 2.5% for the repayment. The initial monthly interest to be paid therefore amounts to 620,025 euros * 0.0265 / 12 = 1,369.22 euros. The initial repayment corresponds to EUR 620,025 * 0.025 / 12 = EUR 1,291.72. A total monthly installment of EUR 1,291.72 + EUR 1,369.22 = EUR 2,660.94 is therefore due. The loan has a fixed interest rate of 15 years.
Calculation of the costs for maintenance and modernization
The simple, but in practice probably significantly underestimated calculation of the provisions for maintenance would in this case be 1 euro / square meter / month * 115 square meters = 115 euros / month. Since I do not know the actual production costs per square meter, I estimate 2,000 euros / square meter. According to Peters' formula, this results in maintenance costs of 2,000 euros * 1.5 / 80 / 12 * 115 = 359.38 euros per month. Based on Gerd Kommer's assumption, the maintenance costs would be between 287.50 euros and 479.17 euros. As the house was built in 2020 and is not detached, we take the lower end and calculate maintenance costs of EUR 287.50 per month. We do not expect any necessary modernizations in the next few years, which is why we only set aside 12.50 euros for this and round the amount up to 300 euros.
Monthly burden on the buyer and residual debt after 15 years
Buyers must transfer 2,660.94 euros per month to the bank in the first 15 years. Added to this are 300 euros for provisions, which increase annually with an assumed inflation rate of 2%. In the first year, the total charge is therefore 2,660.94 euros + 300 euros = 2,960.94 euros. In the last year of the term of the first loan, the maintenance costs amount to 300 euros * 1.02^14 = 395.84 euros. In the last year of the loan, the buyers therefore pay 2,660.94 euros + 395.84 euros = 3,056.78 euros. The remaining debt, as it can be calculated with https://www.zinsen-berechnen.de/kreditrechner.php or Excel, for example, amounts to 334,902.69 euros after these 15 years
Development of the tenant's assets in the first 15 years
At the beginning, the tenant invests his equity (EUR 200,000) less the deposit (EUR 4,400) of EUR 195,600 in his global portfolio. We assume that one unit costs EUR 10 at this point and that the tenant therefore acquires 19,560 units. This is important for the subsequent determination of profit on withdrawal. The difference between the basic rent and the purchase costs in the first year is EUR 2,960.94 - EUR 1,970 = EUR 990.94. This is also paid into the world portfolio every month at a rate of 10 euros. After one year, EUR 195,600 + 12 * EUR 990.94 = EUR 207,491.28 will have been accumulated. We assume an average performance of 6% per year, which means that the value of the portfolio increases to EUR 207,491.28 * 1.06 = EUR 219,940.76 after one year.
The tenants calculate with annual rent increases of 2.2%. The rent in the second year is therefore EUR 1,970 * 1.022 = EUR 2,013.34. As the buyer simultaneously adjusts his provisions by 2% in line with inflation, the tenant can only invest EUR 2,660.94 + EUR 300 * 1.02 - EUR 2,013.34 = EUR 953.60 per month in the second year. At the same time, of course, the price for a share in the global portfolio has risen from 10 euros to 10.60 euros. For the EUR 953.60, the tenant therefore receives 90.82 units per month. Including the 6% performance, the tenant's assets will increase to (EUR 219,940.67 + EUR 953.60 * 12) * 1.06 = EUR 245,266.90 at the end of the second year.
If the calculations are continued, the rent in the 15th year amounts to EUR 1,970 * 1.022^14 = EUR 2,671.65, which still gives the tenant a monthly investment of EUR 3,056.78 - EUR 2,671.65 = EUR 385.13. At the end of these first 15 years, the tenant's assets in the world portfolio increase to approx. 690,435 euros. How is it possible to generate such high assets with just EUR 195,600 in starting capital? The compound interest effect helps. The 195,600 euros alone have grown to 195,600*1.06^15 = 468,766.78 euros over 15 years. In addition, there are the monthly payments totaling over 125,000 euros, which of course also earn interest.
Monthly payments of the buyers and remaining debt in the years 16 to 30
In order to repay the remaining debt of 334,902.69 euros, the buyer takes out another loan with a 15-year fixed interest rate after 15 years. The nominal interest rate has now risen from 2.65% to 4%. In order for the loan to be paid off after 15 years, the buyer must make a repayment of 4.876%. This means that 334,902.69 * 0.04 / 12 = 1,116.34 euros of interest must be paid each month at the beginning, while 334,902.69 * 0.04876 / 12 = 1,360.82 euros are repaid. The monthly installment therefore amounts to EUR 2,477.16. Costs for maintenance and modernization are calculated unchanged and amount to EUR 395.84 * 1.02 = EUR 403.76 per month in the 16th year, resulting in a total monthly charge for the buyer of EUR 2,880.92.
Over the next 15 years, the provisions to be made increase to 403.76 euros * 1.02^14 = 532.75 euros, resulting in a total charge of 532.75 euros + 2,477.16 euros = 3,009.91 euros in the last year of the loan term. After these 15 years, there is a residual debt of 18.40 euros. These are paid off by the buyer by drinking one less beer on his weekly pub night (inflation sends its regards).
Development of the tenant's assets in the years 16 to 30
In the 16th year, the rent rises - as in previous years - by 2.2% to EUR 2,671.65 * 1.022 = EUR 2,730.43. As this is still below the EUR 2,880.92 that the buyer would have to pay in the 16th year, the tenant can continue to save. However, only 2,880.92 euros - 2,730.43 euros = 150.49 euros. The tenant can still pay money into his world portfolio in the 17th and 18th year. After 18 years, the value amounts to approx. 826,376 euros. The increase in value is now almost exclusively due to the return on the portfolio, while the deposits only have a minor impact. Even without further deposits, the value of the portfolio would have increased to EUR 690,435 * 1.06^3 = EUR 822,319.32 over these 3 years.
Things get interesting in the 19th year. In this year, the rental costs of EUR 2,730.43 * 1.022^3 = EUR 2,914.63 exceed the buyer's expenses of EUR 2,477.16 + EUR 403.76 * 1.02^3 = EUR 2,905.63 by EUR 9 per month for the first time. This means that money must now be withdrawn from the custody account every month. One share of our ETF is now worth 10 euros * 1.06^18 = 28.54 euros. In order not to make the calculation any more complicated and because tax matters can change significantly in the years leading up to the withdrawal, we have to estimate the taxes and choose the current tax rate for capital gains of 26.375% (including solidarity surcharge). We assume that the tenant is not subject to church tax and has already exhausted his annual tax-free allowance through other capital investments. We also ignore the possible partial exemption of 30% of the profit. The shares are sold according to the FiFo principle.
As a share is now worth EUR 28.54, we have to sell a share to pay the EUR 9. We were able to buy any number of shares for 10 euros in the first year, which is why the profit per share is 28.54 euros - 10 euros = 18.54 euros. After tax, this means that EUR 10 + EUR 18.54 * (1 - 0.26375) = EUR 23.65 is paid out. Of this, 9 euros are paid, leaving 23.65 euros - 9 euros = 14.65 euros. Naturally, this EUR 14.65 is reinvested and increases the ETF's holdings by EUR 14.65 / EUR 28.54 / unit = 0.513 units. In the first month of the 19th year, the value of the custody account has therefore fallen to EUR 826,376 - EUR 28.54 + EUR 14.65 = EUR 826,362.11. The EUR 9 withdrawal cost the tenant EUR 13.89 in real terms. Accordingly, the value of the deposit is reduced over the course of the year to EUR 826,376 - EUR 13.89 * 12 = EUR 826,209.32. However, as a return is of course also generated this year, a significant plus is recorded at the end of the year, namely EUR 826,209.32 * 1.06 = EUR 875,781.88.
The tenant must also withdraw a steadily growing sum from his global portfolio in the remaining years. In the 30th year, the rental charge rises to EUR 3,702.90, which is EUR 692.99 higher than the buyer's charge. In order to settle this amount, 17 shares must be sold each month at 54.18 euros each. The remaining good 30 euros are of course reinvested. Nevertheless, the tenant's assets increase to approx. 1,582,372 euros by the end of the 30th year.
Interim balance sheet
Before we take a look at the next 30 years, let's take a look at the development of the two assets:
1) Value of the property
The property has always been well maintained, which is why the reserves were set aside. We can therefore assume an increase in value, which we estimate at 2.6% per year: 750,000 euros * 1.026^30 = 1,619,877.18 euros. Of course, we have also carried out modernizations. We initially saved 300 euros for this - 287.50 euros = 12.50 euros per month. Like the maintenance costs, these were increased by 2% each year. For the sake of simplicity, we assume that the modernization reserves flowed directly into modernization projects and subsequently also led to an increase in value of 2.6% per year. This means that after 30 years, the value of the property has increased by EUR 12.5 * 12 * 1.026^30 = EUR 323.98 as a result of the modernizations in the first year. The modernizations in the second year resulted in an increase in value of 12.5 euros * 1.02 * 12 * 1.026^29 = 322.08 euros. Overall, this results in an increase in value of 8,938.37 euros with investments of 6,085.21 euros. The value of the property after 30 years therefore amounts to 1,619,877.18 euros + 6,085.21 euros = 1,625,962.39 euros.
If the buyer wishes to sell the property, further fees will of course be incurred. As the property has already been paid off in full, no prepayment penalty is due, nor does the land charge have to be deleted. A broker's commission of 3.57% is payable on the sale, i.e. 1,625,962.39 euros * 0.0357 = 58,046.86 euros. In addition, an appraisal is prepared for which 0.5% of the market value is charged, i.e. 1,625,962.39 euros * 0.005 = 8,129.81 euros. As the property has been used by the owner throughout, no taxes are due on the sale. The "odds and ends" (energy certificate etc.) are valued at a flat rate of 500 euros. The buyer can therefore realize 1,625,962.39 euros - 58,046.86 euros - 8,129.81 euros - 500 euros = 1,559,285.72 euros from the sale.
2) Value of the securities account
As already calculated, the tenant was able to build up a deposit of EUR 1,582,372 in the same period, the sale of which would of course still incur taxes.
3) Will the value of the custody account rise or fall?
In fact, the value of the custody account increases continuously and in the 30th year from approx. 1,503,493 euros to 1,582,372 euros.
After 30 years and full payment of the property, the tenant and buyer have similar assets, even if the buyer is slightly ahead.
Comparison after 60 years
In the 31st year, the costs for the buyer fall significantly. The loan has been paid off and only reserves for maintenance and modernization need to be set aside. Initially, these costs amount to EUR 543.41 per month and rise to EUR 965.01 per month by the 60th year. Over the same period, the rent payable rises to up to EUR 7,133.27, which is EUR 6,148.26 above the monthly costs of the buyer.
1) Value of the property
The value of the property will increase to EUR 3,534,165 within 60 years, including any modernization work carried out. At this point, the property will probably no longer be sold, but only inherited. Sales costs are therefore not taken into account at this point.
2) Value of the deposit
The value of the securities account in the 60th year is EUR 3,609,298. Here too, a sale is probably no longer on the cards. Only an inheritance appears to make sense.
3) Will the value of the custody account rise or fall?
Even if the monthly costs of the tenant are more than 7 times higher than those of the buyer, the value of the custody account actually increases by a good EUR 100,000 from EUR 3,504,517 to EUR 3,609,298 in the 60th year.
Although the tenant is slightly ahead after 60 years, the difference is negligible. Due to slightly different parameters, the property owner could also take the lead. So in this respect it is actually a draw. However, by buying a property, the buyer is taking a considerable bulk risk and can only use his assets very inflexibly. In addition, the high value of the tenant's deposit is noticeable, which continues to develop positively and thus enables flexible additional consumption. Accordingly, the tenant has fared better in this scenario.
Incidentally, assuming inflation, the 3.5 million euros in 60 years correspond to a current purchasing power of just over one million euros.
Scenario 2: Longer fixed interest rate, but higher interest rate
What happens if we assume a 30-year fixed interest rate and full repayment instead of a fixed interest rate with only 15 years and follow-up financing? In this case, we would probably be offered a loan with an interest rate of 3.5% today. The repayment would be approx. 1.889% and amount to approx. 2,784.43 euros per month - significantly higher than the monthly installment in scenario 1.
The value of the property naturally remains unchanged in this scenario. However, the value of the tenant's deposit increases to approx. 4.7 million euros. In scenario 2, the tenant is again the winner.
As this scenario makes less economic sense (at least if we assume a loan interest rate of around 4% for follow-up financing), the idea of a longer fixed interest period is rejected in the following scenarios.
Scenario 3: Faster repayment of the follow-up financing
As income is also very likely to increase over time, it may be possible for the buyer to repay the loan in just 10 years instead of 15. For a repayment in 10 years, with an unchanged interest rate of 4%, the repayment rate is 8.149%, which corresponds to a monthly installment of 3,390.61 euros.
In this scenario, the final value of the deposit would fall to a good EUR 3.5 million, but would grow into its 60th year. As the value of the property and that of the deposit do not differ significantly, but the value of the deposit continues to rise and offers greater flexibility with less risk, the tenant also wins the comparison in scenario 3.
As scenario 3 is more likely than scenario 1, it will serve as the basis for the following scenarios.
Scenario 4: No annual rent increases, reduction in provisions in old age
Many tenants do not receive annual rent increases. In this scenario, we therefore assume that the rent is only increased every 4 years, but then directly by 1.022^4 ~ 9.09% - i.e. the value that would have resulted from an annual rent increase of the assumed 2.2% after 4 years. The rent in the 4th year is therefore EUR 1,970 * 1.022^4 = EUR 2,149.17 - the same value as in the previous scenarios. Only in the years before that, only 1,970 euros are calculated.
At the same time, some buyers will certainly no longer extensively renovate their property in the last few years, but only repair what is absolutely necessary. Accordingly, we reduce the reserves for maintenance and modernization to 50 euros / month 10 years before the end of the period under consideration. These 50 euros/month will of course continue to be adjusted for inflation. As the property loses value due to inadequate maintenance, I assume an annual increase in value of 0.5% for the last 10 years instead of the 2.6% in the first 50 years.
The value of the property after 60 years thus amounts to approx. 2.9 million euros, that of the deposit to approx. 4 million euros with continuous value growth. Scenario 4 thus also goes - very clearly - to the tenant. In the following scenarios, we continue to assume that the buyer reduces its provisions in recent years and that rent increases are only implemented every 4 years or when the tenant moves.
Scenario 5: The tenants live in a property that suits them
A tenant will repeatedly increase or decrease the size of the rental property over the course of their life and thus adapt it to their circumstances. The buyer, on the other hand, will tend to stay in the property once purchased and choose a size when buying that is suitable for the maximum number of people who are to live in the property. In this scenario, nothing changes for the buyer. The tenants, on the other hand, stay in their old 4-bedroom, 100-sqm rented apartment for the first 5 years before renting the large house. After the children - 20 years later - leave the house in their early 20s and move to another city, the tenants decide to move back into a perfectly adequate 3-room apartment with 90 square meters.
For the sake of simplicity, I convert the price per square meter of the apartment building to the 4- and 3-room apartments. Moving from the 4-room apartment to the house costs 2,000 euros and from the house to the 3-room apartment 3,000 euros. In addition, there are apportionable costs in the rental apartments of initially 25 euros / month for the maintenance of an elevator and the like. These 25 euros are of course adjusted upwards over time with the remaining rent.
The rent for the first 4-room apartment is therefore EUR 1,970 / 131 sqm * 100 sqm + EUR 25 = EUR 1,528.82 and will be increased to EUR 1,528.82 * 1.022^4 = EUR 1,667.86 after 4 years. The deposit is 4,000 euros. After 5 years, the tenant moves into the house, the rent for which has now risen to 1,970 euros * 1.022^5 = 2,196.45 euros. There are also one-off moving costs of 2,000 euros. The deposit for the house is now 5,500 euros, i.e. an additional 1,500 euros must be withdrawn from the tenant's deposit. Here too, the rent is increased by 9.09% every 4 years. After the house has been occupied for 20 years, the tenant moves into the 3-room apartment at a rent of (1,970 euros / 131 sqm * 90 sqm + 25 euros) * 1.022^25 = 2,374.97 euros plus one-off moving costs of 3,000 euros. The deposit for this 3-room apartment amounts to 5,500 euros and will be financed entirely from the previously returned deposit.
The value of the purchased property remains unchanged at approx. 2.9 million euros. The value of the deposit is approx. 7 million euros and has of course been growing inexorably in recent years. A clear victory for the tenant.
Scenario 5 is - in my view - the most realistic scenario to date and therefore serves as the basis for scenario 6.
Scenario 6: The buyer also moves
If the buyer is able to part with his cherished property, he will also look for a property that is better suited to his life situation over time. The buyer therefore also sells his house after 25 years and buys a more suitable 3-room apartment with 90 square meters. Here too, for the sake of simplicity, we calculate the price per square meter of the house down to the 3-room apartment and multiply by the expected increase in value to determine the price of the apartment. 750,000 euros / 115 square meters * 90 square meters * 1.026^25 = 1,115,038.73 euros. Thanks to the buyer's negotiating skills, the apartment changes hands for 1 million euros. There is also a 3.57% estate agent's fee, 1.5% notary fees, 0.5% for the land register entry, 3.5% land transfer tax and 2,000 euros for an expert. A total of 1,092,700 euros
On the other hand, the value of the house to be sold is 750,000 euros * 1.026^25 = 1,424,771.71 euros. As the buyer has regularly invested money in modernization, the sales price increases by a further 6,891.74 euros to 1,431,663.45 euros. Brokerage fees of 3.57%, costs for a valuation report of 0.5% and "small items" over 500 euros must be deducted from this. 1,431,663.45 euros * (1-0.0357-0.005) - 500 euros = 1,372,894.75 euros.
After purchasing his new apartment and relocation costs of EUR 3,000, the buyer still has a plus of EUR 277,194.75, which he invests in a global portfolio at the same conditions as the tenant. The monthly maintenance costs for the buyer naturally decrease, but must be paid to the condominium association until the end of the period under consideration. In addition, there is an initial EUR 20 for non-recoverable costs such as property management. Instead of 482 euros, which the buyer last set aside for the house, the costs fall to 300 euros + 20 euros = 320 euros.
As both the tenant and the buyer live in an apartment after 25 years, we can simplify the calculation somewhat and dispense with the consideration of apportionable ancillary costs that are only incurred for apartments (e.g. operating costs for an elevator). The relevant ancillary rental costs for the 3-room apartment are therefore reduced accordingly.
In this scenario, the tenant has access to a good EUR 6.9 million in the deposit at the end of the period under consideration, which of course grows significantly until the last year. The buyer's deposit has grown to a good EUR 2.1 million in the same period. His apartment is now worth around 2.5 million euros. However, even in this scenario, the buyer's total assets of around 4.6 million euros are significantly lower than those of the tenant.
End of part 2
From my point of view, scenarios 5 and 6 are the most likely. At least that's how I would behave as a buyer or tenant. Accordingly, the tenant wins more than clearly. Under the current framework conditions and the assumptions made, it makes no financial sense to buy a property in Regensburg or comparable regions. In the next part, we will look at how these framework conditions and assumptions would have to change for the buyer to make the better financial decision after all.
Are the assumptions unrealistic for you? Is the housing situation different in your region? That is quite likely. You are welcome to share more realistic assumptions and framework conditions in the comments. I'll do the math for you in part 3. You can find part 3 here: https://app.getquin.com/activity/GEBmMewkKS
Do you think scenarios 5 and 6 are unlikely? Let me know in the comments what seems more realistic to you!
Even though I have checked my calculations several times, there is always a chance that an error has crept in. If you've found one, can't understand a calculation step or simply have a question about the calculation => let me know in the comments!
#mieten
#eigenheim
#esel
#alternative
#learn